Trampoline Pattern in Java: Mastering Recursion Without Stack Overflow
Also known as
- Bounce
- Tail-Call Optimization
Intent of Trampoline Design Pattern
The Trampoline Pattern in Java optimizes recursive function calls by converting them into iterative loops, avoiding stack overflow errors.
Detailed Explanation of Trampoline Pattern with Real-World Examples
Real-world example
Imagine you are organizing a relay race. Each runner passes the baton to the next runner until the race is complete. However, if each runner had to physically run back to the starting line to pass the baton to the next runner, the race would be inefficient and error-prone. Instead, runners pass the baton directly to the next runner in line, who continues the race seamlessly.
The Trampoline pattern in programming works similarly by ensuring that each recursive step is handed off efficiently without having to return to the start, preventing a stack overflow (similar to our runners never having to backtrack).
In plain words
The Trampoline pattern in Java allows efficient recursion without running out of stack memory, optimizing deep recursive calls for better performance and stack safety.
Wikipedia says
In Java, trampoline refers to using reflection to avoid using inner classes, for example in event listeners. The time overhead of a reflection call is traded for the space overhead of an inner class. Trampolines in Java usually involve the creation of a GenericListener to pass events to an outer class.
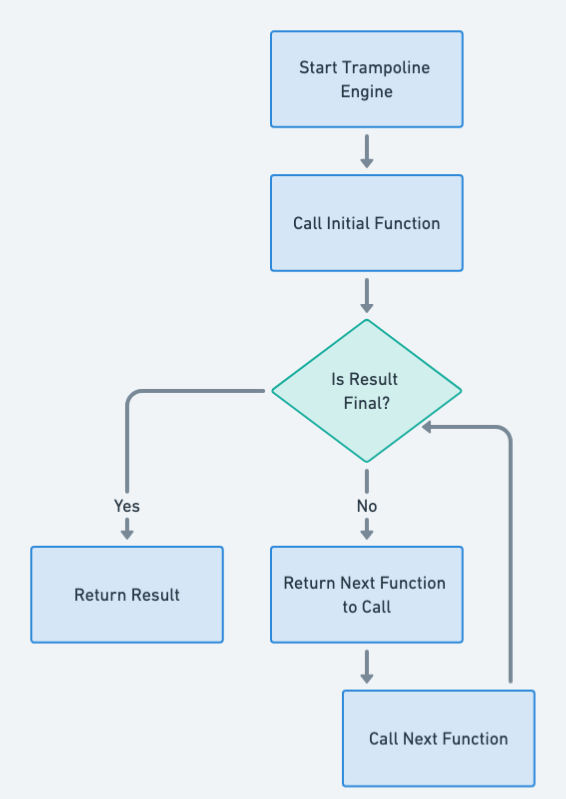
Flowchart
Programmatic Example of Trampoline Pattern in Java
Here's the Trampoline implementation in Java.
When get is called on the returned Trampoline, internally it will iterate calling jump on the returned Trampoline as long as the concrete instance returned is Trampoline, stopping once the returned instance is done.
public interface Trampoline<T> {
T get();
default Trampoline<T> jump() {
return this;
}
default T result() {
return get();
}
default boolean complete() {
return true;
}
static <T> Trampoline<T> done(final T result) {
return () -> result;
}
static <T> Trampoline<T> more(final Trampoline<Trampoline<T>> trampoline) {
return new Trampoline<T>() {
@Override
public boolean complete() {
return false;
}
@Override
public Trampoline<T> jump() {
return trampoline.result();
}
@Override
public T get() {
return trampoline(this);
}
T trampoline(final Trampoline<T> trampoline) {
return Stream.iterate(trampoline, Trampoline::jump)
.filter(Trampoline::complete)
.findFirst()
.map(Trampoline::result)
.orElseThrow();
}
};
}
}Using the Trampoline to get Fibonacci values.
@Slf4j
public class TrampolineApp {
public static void main(String[] args) {
LOGGER.info("Start calculating war casualties");
var result = loop(10, 1).result();
LOGGER.info("The number of orcs perished in the war: {}", result);
}
public static Trampoline<Integer> loop(int times, int prod) {
if (times == 0) {
return Trampoline.done(prod);
} else {
return Trampoline.more(() -> loop(times - 1, prod * times));
}
}
}Program output:
19:22:24.462 [main] INFO com.iluwatar.trampoline.TrampolineApp - Start calculating war casualties
19:22:24.472 [main] INFO com.iluwatar.trampoline.TrampolineApp - The number of orcs perished in the war: 3628800When to Use the Trampoline Pattern in Java
Use the Trampoline pattern when
- When dealing with algorithms that use recursion heavily and risk running into stack overflow errors.
- When tail-call optimization is not supported by the Java language natively.
Trampoline Pattern Java Tutorials
- Laziness, trampolines, monoids and other functional amenities: This is not your father's Java(Mario Fusco)
- Trampoline.java (totallylazy)
- Trampoline: Java Glossary (mindprod.com)
- Trampolining: A practical guide for awesome Java Developers (John McClean)
- What is a trampoline function? (Stack Overflow)
Real-World Applications of Trampoline Pattern in Java
- Implementing algorithms that require deep recursion, such as certain tree traversals, combinatorial algorithms, and mathematical computations.
- Functional programming libraries and frameworks where tail-call optimization is necessary for performance and stack safety.
- cyclops-react
Benefits and Trade-offs of Trampoline Pattern
Benefits:
- Prevents stack overflow by converting deep recursion into iteration.
- Enhances performance by avoiding the overhead of deep recursive calls.
- Simplifies the code by making recursive calls look like a sequence of steps.
Trade-offs:
- May introduce additional complexity in terms of understanding and implementing the trampoline mechanism.
- Requires converting naturally recursive algorithms into a continuation-passing style.
Related Java Design Patterns
- Iterator: Both patterns aim to transform potentially recursive operations into iterative processes, though the iterator pattern is more general-purpose.
- State: Like the Trampoline, the State pattern can also handle complex state transitions, which can sometimes involve recursive-like state changes.
- Strategy: This pattern can be related in terms of defining a family of algorithms (or continuations in the case of the Trampoline) and making them interchangeable.